疾病检测与贝叶斯公式

18 Aug 2014

---

在医院，如果医生怀疑你得了某种疾病，一般会让你做一些检查，而检查结果往往有阴性、阳性之分。通常我们不希望是阳性，因为阳性可能意味着你体内存在某种病毒（菌）。在一些重大疾病的检测中，如果我们看到结果是阳性，就感觉自己被判了死刑，十分恐慌。

假设有一种设备，可以通过对血液样本的检测（结果有阳性和阴性）来判断你是不是一位艾滋病患者。¹如果你是一名艾滋病患者，那么经过检测后，结果显示为阳性的概率为99$\%$ 。如果你并没有携带艾滋病毒，经过检测后，结果显示为阳性的概率仅为1$\%$ 。也就是说，这种设备较为可靠，不论你是否患有艾滋病，它基本能作出正确的判断。假如现在，用艾滋病检测试纸对自己进行一次检测，检测结果显示是阳性，那请问你觉得自己得艾滋病的概率是多大？你会不会害怕？我曾经与同门讨论这个问题，大家都认为，既然这种设备这么准确，而且检测结果又是阳性，那么肯定是患有此病！

果真如此吗？无论是否学过统计，对这个问题，许多人存在判断误区。其实，即使检测结果是阳性，到底有没有患病还要看这个病本身在人群中是否罕见。接下来我们通过一个简单的图示来解释这个问题。

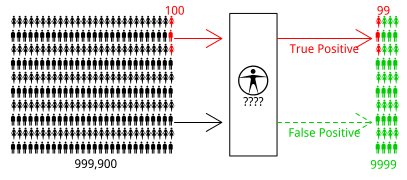
图1:即使为阳性，也不必过分恐慌²

我们直接从总体出发，假设总人口是1000000,患艾滋病的概率是1/10000 。³因此平均说来，在该人群中，只有100 人患病（图1左侧右上方红色小人），而另外999900 人不患病（图1左侧黑色小人）。现在，人群中每个人用检测试纸检测 自己的血液。对100 名患者而言，由于检测成功率为 99$\%$ ，大致有99 人检测结果呈阳性（如图1 右侧左上方红色小人）。有病并且能真正检测出来，我们称之为正确发现（True Positive）。虽然该台设备检测成功率很高，但是也必须考虑其失败的情形，检测失败意味着这个人没病，但检测结果呈阳性。⁴对999900名正常人而言，虽然该台设备检测失败概率仅为1$\%$，但由于接受检测的人基数很大，所以平均来说9999 人检测结果呈阳性。没病却检测为有病，我们称之为错误发现（False Positive）。

False Positive True Positive

当所有人检测完毕，形成了一个检测结果为阳性的群体（如图1右侧部分）。在这个群体中，并非全是真正的患病者，甚至可以说，绝大多数人（图1右侧绿色小人）都不是患病者!为什么呢？因为虽然接近10100人的检验结果呈阳性，而真正患病人数仅有100人（图1右侧左上角红色小人），概率为1$\%$。因此得到一个自然的结论：当随机从总体中抽出一个人，利用检测试纸进行检测，如果检测结果呈阳性，并不意味着这个人一定患病，他患病的可能性仅有1$\%$。

图1的背后的统计原理是贝叶斯公式。假设$H$代表患病，$H’$代表不患病，$A$代表检测结果为阳性。根据背景知识，我们有： 人群中某人患病概率$P(H)=1/10000$，不患病的概率$P(H’)=9999/10000$，患病条件下检测结果呈阳性概率$P(A|H)=99/100$，不患病条件下检测结果呈阳性概率为$P(A|H’)=1/100$。若某人检测结果为阳性，利用贝叶斯公式来计算其患病概率：

计算结果与图1结论相符。我们不禁要问，既然检测结果呈阳性，仍然不能判断这个人是否患病，那么检测价值何在？检测当然是有价值的！我们注意到，从人群中随机抽出的一个人，其患病概率为1/10000，如果其检测结果呈阳性，其患病概率会提高100倍，变为1/100。这就是检测的价值所在：利用检测的结果可以更新先验概率（把普通人患病概率1/10000 称作先验概率）得到后验概率（得知检测结果为阳性的患病概率1/100称为后验概率）。这个后验概率又可以作为下一次检验的先验概率，也就是说，如果想进一步确定这个人的患病情况，可以对其做其他检测，也就意味着对1/100 这个概率做进一步的更新。

本文PDF版。

---