画一条平滑曲线

10 Jul 2013

---

“魔鬼就在细节里”，所言不虚。如何画一条平滑的曲线，看似一个简单的问题，动手来做，就会发现没有你想象的那么简单。

比如下面这张图：

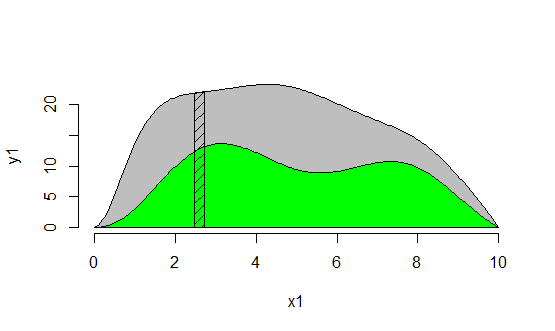
可不可以用诸如Picaso、photoshop或者微软自带的画图软件来做呢？我想除非是行家，否则不要走这条路。更何况，如果你还要实现对图更加细微的控制的话，就更不要走那条路了。可行的方案是，把你所要画的曲线用函数来表示。常用的就是把它用高次函数来表达：

\[y = b_{0} + b_{1}x + b_{2}x^2 + \ldots + b_{n}x^n\]

如果n越大，那么画出的图形就越细致。什么意思呢？如果n=1,这就是一条直线了，一个弯也拐不了；如果n=2,这就是一条抛物线，可以拐一个弯；如果n=3,曲线就更复杂，最多可以拐两个弯。一条曲线复杂与否，就与它拐弯的次数有关。所以要描述一条复杂的曲线，我们需要一个一元高次函数。

问题随之而来，如果确定与一条曲线相对应的高次函数呢？你可能会想，我们可以利用函数的性质，来确定一个函数的各个参数。然后你就开始调这个函数的各个系数，你的目的是调到函数曲线和目标曲线一致为止。

\[y = b_{0} + b_{1}x + b_{2}x^2 + \ldots + b_{n}x^n\]

对于抛物线或拐两个弯的三次函数曲线可以这样做，但对于稍微复杂一点的曲线，这同样是一条不归路。

如何获得与你心目中的曲线相对应的函数曲线呢？可以这样做：

1. 随手画出你的曲线（可能一点也不平滑）；
2. 用高次函数拟合这条曲线；
3. 拟合的结果即为你想要的曲线所对应的函数；
4. 用该函数生成一条平滑曲线。

以上步骤我们力求在R中实现。

对于第一步，需要定义R绘图窗口的事件控制。

mousedown<-function(buttons,x,y)   
{
  if(buttons==2) return(invisible(1))
  px<-c(px,x)
  py<-c(py,y)
  #devset()
  eventEnv$onMouseMove<-mousemove
  NULL
}
mousemove<-function(buttons,x,y)
{
  px<<-c(px,x)
  py<<-c(py,y)
  # devset()
  grid.points(x,y)
  NULL
}
mouseup<-function(buttons,x,y)
{
  eventEnv$onMouseMove<-NULL   
}

mousedown()的作用是一旦你在绘图窗口上按下鼠标，就会将所在位置的横纵坐标提取出来存入变量(px,py)中。mousemove()的作用是鼠标一旦发生移动，不仅会将移动位置的坐标提取出来，还会将这些点画出来。mouseup()不进行处理。注意到，所提取的坐标均是0至1之间的数。

下面，打开一个图形窗口并定位一个图层：

pushViewport(viewport())
px <- NULL
py <- NULL
setGraphicsEventHandlers(onMouseDown=mousedown,
                         onMouseUp=mouseup,prompt='Start to write')
eventEnv<-getGraphicsEventEnv()

getGraphicsEvent()

现在可以鼠标在图形窗口拖动画出你想要的曲线的大致形状。

对坐标稍加变换,然后用曲线回归进行拟合：

x <- 10*px
y <- 30 *py
rhs <- function(x, b0, b1, b2, b3, b4, b5, b6) {
  
  x*(b0 * x + b1 * x^2 + b2 * x^3 + b3 * x^4 + b4 * x^5 + b5 * x^6 + b6 * x^7)*(x-10)
}
ds <- data.frame(x = x, y = y)
m1 <- nls(y ~ rhs(x, b0, b1, b2, b3, b4, b5, b6), data = ds)

其中x*(b0 * x + b1 * x^2 + b2 * x^3 + b3 * x^4 + b4 * x^5 + b5 * x^6 + b6 * x^7)*(x-10)可以确保曲线经过（0,0）和（10,0）点。这可以算是对曲线的一种常见的要求，其实现就是依靠乘积项”x*(x-10)”。

曲线拟合完成后，我们直接在m1基础上进行预测，形成一条平滑曲线：

x1 <- seq(0, 10, length = 200)
par(mfrow = c(1, 2))
plot(x, y, type = "p")
plot(x, y, type = "n")
lines(x1, predict(m1, list(x = x1)), col = "2", lwd = 3)

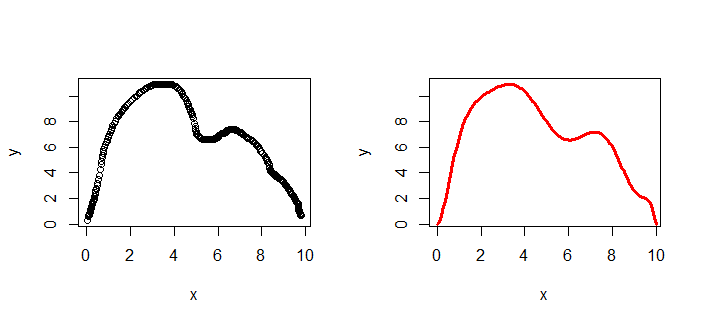
这样，我们就得到了一条心目中的平滑曲线。最为关键的是可以对这条曲线进行细微的控制。如下图，我们添加一个细分：

y1 <- predict(m1, list(x = x1))
plot(x1, y1, type = 'n', axes = F)
axis(1)
axis(2)
polygon(x1, y1, col = "grey")
polygon(x1[c(50, 50, 51:55, 55)], c(0, y1[50:55], 0), border = 1,
   density = 10, angle = 45)

---